CPSC120B
Fundamentals of Computer Science I

Lab 13

Function Scope

Write a function called equilateral_area(edge_length) that computes the area of an equilateral triangle with the specified edge length.

\[area = \frac{\sqrt{3}}{4} \times length ^ 2 \]















  
 
    Copy and paste your solution to the previous exercise into
    this one,
    and use it when writing a function
    called sierpinski_area(edge_length) that computes
    the
    area of a Sierpinski triangle of order one.  A Sierpinski
    Triangle of
    order one is an equilateral triangle with a triangular hole.
    The
    vertices of the hole triangle are the mid points of the
    Sierpinski
    triangle's edges.  For example:
  

  

    
  

  

    Note: The editor boxes on this page use the Emacs
    shortcuts for copy and paste.  Copy is Alt-W (M-W), and paste is
    Ctrl-y (C-y).
  



  


  

  

    
  

  





Trees



  When working with functions, abstraction is key.  You will soon find
  yourself in a position where you start thinking about problems in
  functions.  Being able to break a complex problem, like an advanced
  drawing, into smaller and simpler problems which can be solved with
  a function can make your code a lot easier to write, and a lot
  easier to read.



Details



  Create a function draw_tree(x_location, y_location) in
  a file called forest.py.  The function should use
  the graphics
  module to draw a tree.  The x and y location specified is the center
  of the base of the triangle making up the tree. The tree should
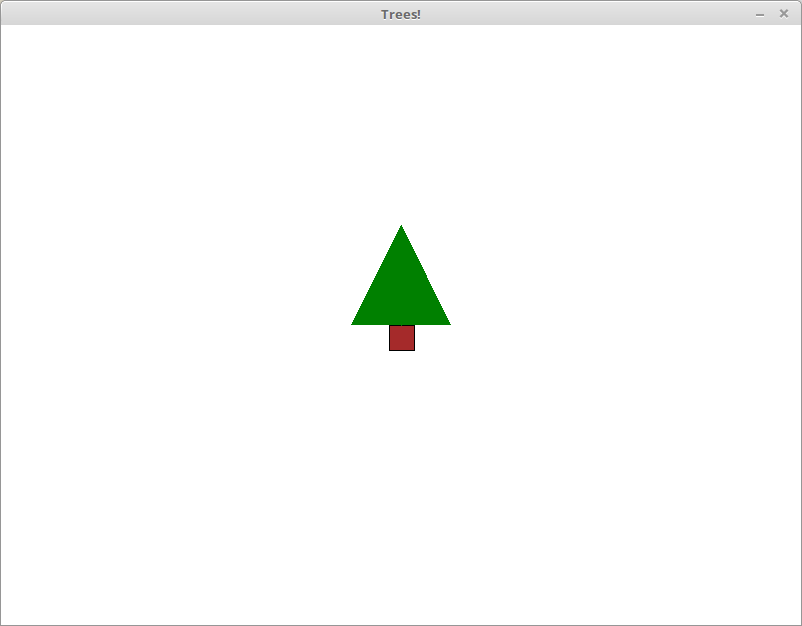
  look like the tree in the example below.




  Notice that a tree is defined by a brown square, and a filled green
  triangle.  For this, define one additional
  function in the same file.  This second function should be
  called
  draw_triangle(x_location, y_location),
  which creates a filled, green isosceles triangle of some globally
  defined height.  For this triangle, the height of the triangle is the
  same as the length of the base of the triangle.





  Note that there is no mechanism for drawing a filled triangle using
  the graphics module.  You can simulate drawing a filled triangle by
  drawing several lines from the apex of the triangle to the base of
  the triangle.  If you specify the line thickness accordingly, you
  will end up with a filled triangle.





  Test your function by calling the function multiple times with
  different parameters.  Make sure your code follows the course's code
  conventions.



Example Output


graphics.window_size(640, 480)
draw_tree(320, 240)


Turtle Drawing of a Tree



Hint



  
  

    
    
      
  • 
	Your draw_tree function should consist basically
	of one call to draw_rectangle from the graphics
	module, and one call
	to draw_triangle (which you are also writing in
	this file).
      
    • 
      
  • 
	An isosceles triangle is a triangle where two of the sides
	have the same length.  For our particular version of an
	isosceles triangle, we will say that the two vertical sides
	have the same length.  The height of the triangle will be
	exactly the same as the width of the triangle.
      
    • 
      
  • 
	To fill in the triangle, you will compute a series of x coordinates
	along the base of the triangle.  You can use a for loop to
	generate these x coordinates.  Inside of this loop, you will
	call draw_line to connect the top of the triangle
	to the corresponding point at the bottom of the triangle.  The
	following image is what the tree would look like if we skipped
	drawing some lines: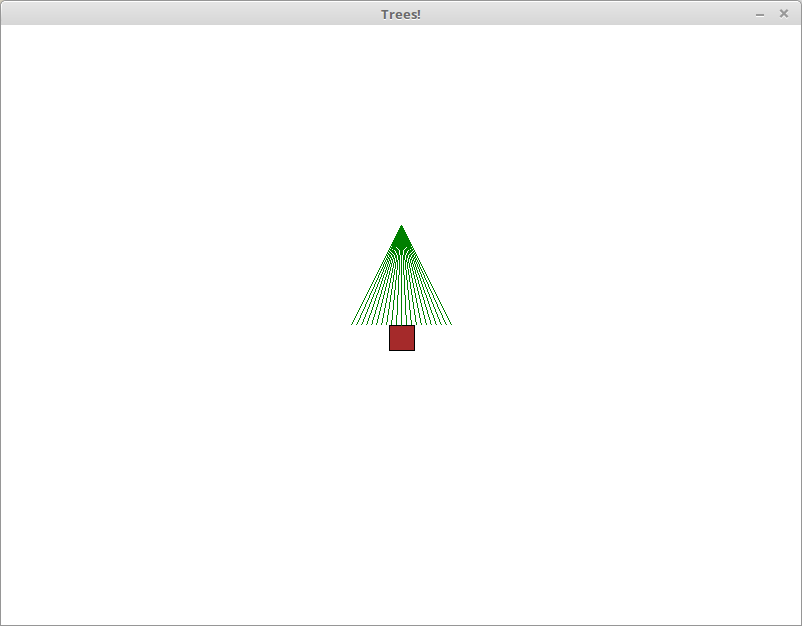

	Turtle Drawing of a Sparse Tree

      
    • 

    

  






  
Challenge

  

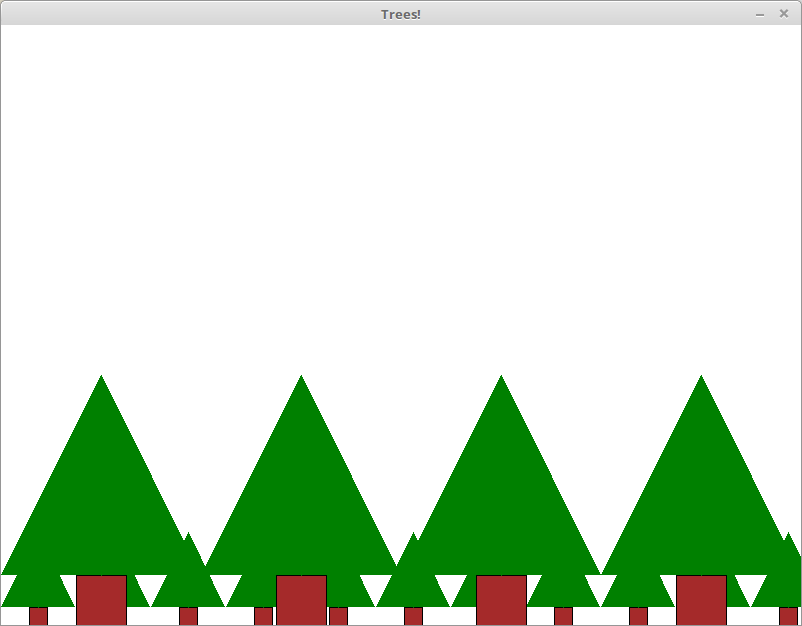
    Modify your program so that you can specify the size of the tree.
    We will define the size of the tree to be the witdh of the tree
    (and the height of the triangle).  Use this new function to draw
    yourself a forest of trees.
  

  Turtle Drawing of a Forest





Submission


Please show your source code and run your programs for the instructor or lab assistant. Only a programs that have perfect style and flawless functionality will be accepted as complete.