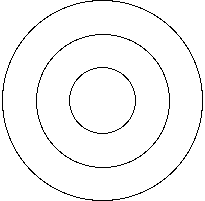
In a file called practice.py, create a function
called draw_target(center_x, center_y, size). This function
should use the graphics
module's draw_oval function to draw a series of 3
concentric circles centered at the specified x and y location.
The radius of the external circle is specified by the size
parameter. The radius of each circle decreases by 1/3 the original
radius each time.
Example
Creating an animation on a computer screen is fairly comparable to the way that flip-book animations work. In a flip book, you draw your image in one location, and on the following page you draw your image in a new, updated location. The analogue to flipping the page using the graphics module is clearing the screen. We then just need some mechanism to continually update the position of the image that we are drawing between screen clears.
Details
Create a python program in a file called floating.py. You
should create a function called
move_image(image_name, start_x, end_x, y_location),
which will animate an image moving horizontally across the screen from the
specified start_x location on the screen to
the end_x location along the specified y_location.
Example
graphics.window_size(320, 240)
move_image("blinky.gif", 0, 340, 180)
You can use the image below that is used in the above example. Or you can use any gif image you want.

Hint
-
The
draw_imagefunction in the graphics module draws an image centered at a specified location. Your image needs to be stored in the same directory as your program. To achieve the motion required here, we just need to change the x coordinate the image every time it is drawn. - You are going to use the range function to accomplish this animation. You at least need to use the 2 argument version of the range function for this, though you can also use the 3 argument version.
- You will either need to use an accumulator, or use the loop variable as the updated value of the x coordinate for the drawn image.
Challenge
Modify your program so that you move not along a horizontal line, but you can move between any two arbitrary (x, y) coordinates.
Example
An Orrery is a mechanical model of the solar system that was first made in the 1700s. A sun was placed in the center of the model, and the orbits of the planets were fixed to a circle surrounding the star. Mimicking the motion that was created with this mechanical device requires using some trigonometry to compute the new x and y positions.
Details
Create a python program in a file called orrery.py. You
should create a function called
animate_planet(radius), which will animate a planet
orbiting around a star in the center of the screen. To compute the
position of the planet, use the following equations to convert an
angle, in radians, to the x and y coordinates of a point on a circle
centered on the origin:
Example
Hint
Create a for loop that iterates over the angular
position of the planet. For each iteration, use the provided
equations to convert the angle to x and y coordinates. Don't
forget to clear the screen and wait to
slow the animation.
The only mathematical issue you may run into is the fact that
the trigonometric functions expect their input in radians
instead of degrees. You can use the math.radians
function to convert from degrees to radians.
Challenge
A real orrery doesn't just have one planet. It usually has many planets, all orbiting at different distances and speeds. Modify your program so that it can animate at least 2 separate planets, at different radii and at different speeds.
Example
Submission
Please show your source code and run your programs for the instructor or lab assistant. Only a programs that have perfect style and flawless functionality will be accepted as complete.