< Back

Lecture 8- Searching and Algorithms

As usual, create a directory to hold today's activities: 

$ mkdir ~/cs170/labs/lab8 
$ cd ~/cs170/labs/lab8

Test Overview

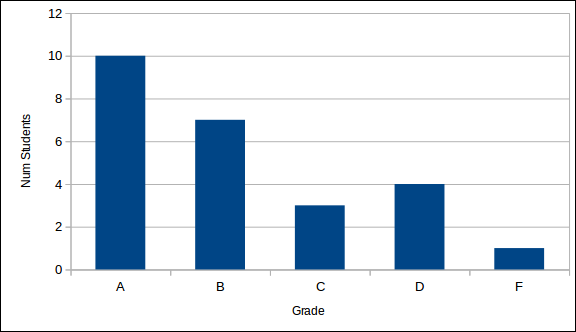
Overall the test went really well. This is a trend that I would request continue! For those of you who are "mathy" and like this sort of thing:

Average
85.55
Median
87.09
Mode
93.54
Standard Deviation
13.38

How to Search

At this point, we have taught you all of the necessary syntax for python to consider yourself "coders." However, being able to code is only part of the way to becoming a real programmer. Being able to program involves being able to plan programs well, and being able to use the most efficient mechanisms possible.

Today, we will talk about two different algorithms for searching. Which algorithm should we use in which scenarios? How do these algorithms compare? Let's explore these, and more.

Lab Activity 1
Linear Search

The most straight forward method of determining if and where some item is in a list is a process known as Linear Search. With linear search, we examine every element in the list starting from the front of the list. If we find the element we are looking for, we return the index. If we look through the entirety of the list and don't find the item, we return some value representing the fact that the element was not in the list.

Details

In a file called searching.py, write a function called linear_search(a_list, a_string). This function takes two parameters: a_list: a list of strings and a_string: a string. This function should return True if a_string is in the list, and False otherwise.

Example

>>> my_list = ["So", "long", "and", "thanks", "for", "all", "the", "fish"]
>>> linear_search(my_list, "thanks")
True
>>> linear_search(my_list, "Ford")
False

Hint

  • You should use a for loop to iterate through elements of the list. You can simply return True when you find the element a_string in my_list.

  • You need to set up a default case, where you have searched through the entirety of the list and have not found the element in question. In this case, you should return False.

 

Challenge

Linear search might take a very long time. However, our computers today are fast enough that even with very large lists we will not notice the difference between this and the other search mechanism discussed today.

Add to your program a function that will create a random list of strings of some specified size. Modify your program so that you use increasingly larger lists. Add a comment in your program which lists the point at which linear search starts taking a noticeable amount of time.

Note that for a fair comparison, you are going to need to always spend the most amount of time searching. What is this worst case going to be, given an arbitrary list?

Lab Activity 2
Binary Search

Binary search is a searching technique that leverages additional knowledge about the contents of the list. Namely, it knows that the items in the list are in some order. If we have items in some order, we can leverage this knowledge of the relationships between elements, in an attempt to speed up our search process.

Details

In a file called searching.py (the same file linear search is in), create a function called binary_search(a_list, a_string). This function takes two parameters: a_list, an ordered list of strings; and a_string, a string. This function should simply return True if a_string is in a_list, and False otherwise.

The steps for binary search are as follows. First, look at the element at the middle of the list. If that item is the string being searched for, you are done. If it is not, then you figure out which half of the list the a_string should appear. If the parameter a_string is less than the middle element, then a_string is in the left half of the list. Otherwise it is on the right. You then continue this process on the appropriate half of the list, until you find a_string. Of course, you also need to stop if you run out of elements to examine.

Make sure you test your code on all of the boundary conditions! It is easy to get the basic gist of this algorithm coded quite quickly, but you need to be able to handle the edge cases well.

To save yourself some time, you can use the sort method of lists, to produce an ordered list of elements.

Example

>>> my_list = ["So", "long", "and", "thanks", "for", "all", "the", "fish"]
>>> my_list.sort() #Remember, lists are mutable.  This sorts in place.
>>> binary_search(my_list, "and")
True
>>> binary_search(my_list, "Ford")
False

Hint

  • You should define two local variables in your function: start and end. These variables are going to represent the beginning and the end of the list you are considering at this point.

  • The arithmetic mean of start and end is the index of the element you are examining at this iteration of the loop. You should store this in a variable called mid.

  • If the element at the current mid index is greater than the search string, then assign mid - 1 to end. If the element at the current mid index is less than the search string, then assign mid + 1 to start.

  • You will need to use a while loop for this, as opposed to a for loop. You will want to stop your loop when start is greater than end.

 

Challenge

If you followed the hint, then you probably stored indicies in variables to determine where in the list you were searching. This is the generally accepted algorithm for binary search, which will work in ALL programming languages.

However, there is usually a more Python-centric version of the algorithms we will be discussing in class. I will always show and discuss the general solution. It will be up to you to figure out the Python version.

You already know of a mechanism that will pull a specific sub-set of elements out of a list. Leverage this technique to simplify your binary search program considerably.

 

Challenge

The true power of binary search is not that it is able to determine if an element is in the list, but how quickly it can do so. The number of comparisons necessary to determine whether or not an item is in a list should be less than that of linear search. Modify your functions so they output the number of comparisons needed to find an element.

Try your new functions with lists of various sizes. Can you define the pattern that emerges, as a function of the size of the list? Does the element being searched for affect your results? Can you find instances where linear is faster than binary?

Submission

When you have finished, create a tar file of your lab8 directory. To create a tar file, execute the following commands:

cd ~/cs170/labs
tar czvf lab8.tgz lab8/

To submit your activity, go to inquire.roanoke.edu. You should see an available assignment called Lab Assignment 8. Make sure you include a header listing the authors of the file.

In-Class Notes