Use the command line to create a new directory called lab8 in your labs directory. Make sure all of the .py files that you create for this activity are in that directory.
Hopefully you are familiar with the sine and cosine functions from back in your trigonometry class. As you can imagine, these are incredibly useful functions not only for mathematics, but for drawing in general. As it turns out, these function in the math module are Fruitful functions: they return the value they compute. Since these functions return their values, we can use those values in our drawings.
Details
Create the function draw_sin(amplitude) in a file
called sine.py. The
function should use the turtle module to draw a function
plot of the math.sin function on the turtle window.
The amplitude parameter is a scaling factor that tells
you how much to inflate the value that the math.sin
function returns.
You will have to modify the input and output of
the math.sin function, so that the sine wave is visible
on the turtle window. Make sure to
test your function by calling the function multiple times with
different parameters. Make sure your code follows the course's code
conventions.
Example
You can place the follwing code at the bottom of your sine.py to check your work.
draw_sin(25)
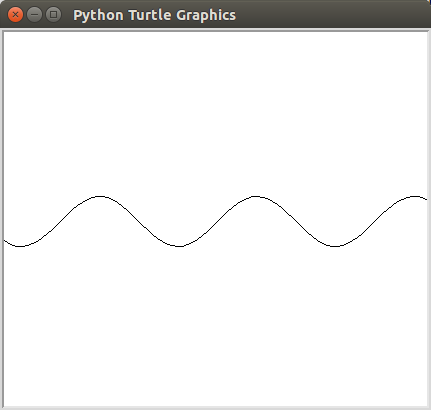
Hint
- You are going to approximate the sine wave curve by simply sampling the sine function. You are going to choose a set of equally spaced points on the curve. Use a for loop that starts at the left part of the window, and increases the value by a fixed step until it gets to the right portion of the window.
-
Treat the input to the
math.sinfunction as the x coordinate of the point on the turtle window, and the return value as the y coordinate. You then simply have togotoeach one of these points in a sequence. -
The
math.sinfunction always returns a value between -1 and 1. You need to use theamplitudeparameter to increase the size of this output, so you can visually see the actual sine wave. You can do this by multiplying the output byamplitude. -
To smooth the sine wave out, divide the input to
the
math.sinby the amplitude as well.
Challenge
The sine and cosine functions are interesting, but I think the tangent function is a much more visually appealing function. Change the color of the turtle's pen, and also plot the tangent function on top of the sine function.
There are many people that would call me a lazy person. I don't find that offensive, but I think it's not a valid description. It's not that I'm lazy, I just try to be as efficient as possible. For example, in college a group of friends and I deduced the fewest amount of coins to carry that would produce any arbitrary amount of change. While a computation like that is still a little too complex, figuring out the fewest amount of coins for a fixed amount of change is possible.
Details
Create the function count_coins(cents) in a file
called change.py. This function should take as a parameter
the number of cents (an integer in the range 0 to 100) and returns
the smallest number of coins (using the American monetary system
consisting of quarters, dimes, nickles and pennies) necessary to
make that amount of change.
Test your function by calling the function multiple times with different parameters. Make sure your code follows the courses code conventions.
Test Cases
| Function Parameters | Expected Output |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 5 | 1 |
| 10 | 1 |
| 15 | 2 |
| 16 | 3 |
| 25 | 1 |
| 50 | 2 |
Hint
- While it might seem like you are going to use a loop for this function, you actually won't use a single loop.
- You can use integer division (//) to determine how many times a coin goes into the change amount evenly.
- Recall that you can use the mod (%) operator to determine the remainder of an integer division operator. Use this to determine the change amount the rest of the coins need to cover.
- Start with the largest coin first (quarters) and work your way down. This is known as a greedy approach, and is very common in Computer Science.
Challenge
Going back to my inspiration for this activity, the perfect amount
of change is going to be the maximum number that this function
will produce on inputs in the range [0,
100). Once your function is written and tested well,
compute the number of coins for all possible change values. Use
the max function to find the largest number of coins.
Submission
Please show your source code and run your programs for the instructor or lab assistant. Only a programs that have perfect style and flawless functionality will be accepted as complete.