Bezier Curves

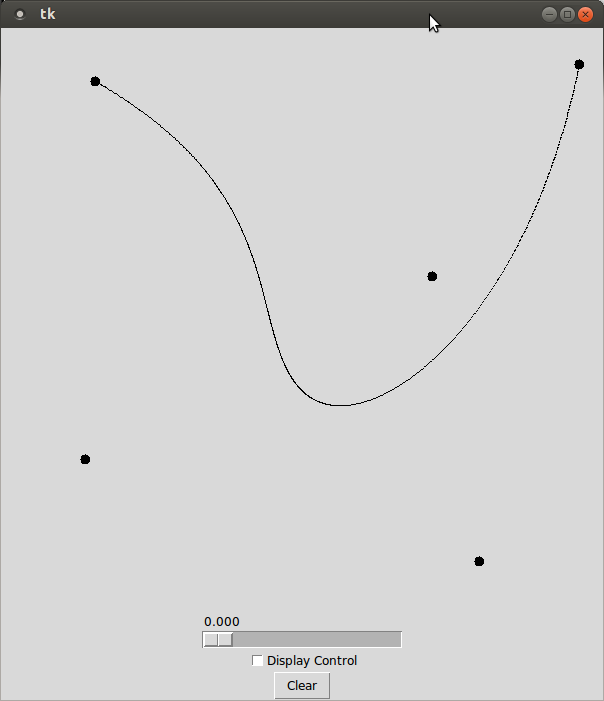
A Bézier curve is a method for representing curves popularized by the French engineer Pierre Bézier in the 1960's. Bézier used the curves in the design of automobiles. The curves are still popular today in drawing and animation applications because they offer an intuitive control over curve shape. Bézier curves can also be approximated very easily using a recursive algorithm developed by another Frenchman, Paul de Casteljau. You are going to create a program that allows users to draw a Bézier curve.

Setup

Create a directory assignment8 under assignments in your cs170 directory. All code for the assignment should be stored in this directory.

  cd ~/cs170/assignments
  mkdir assignment8 
  cd assignment8 

Details

Your program should have a variable at the top of the file called POINTS. This variable should store a list of tuples, which specify a location in 2-dimensional cartesian space. Your program will draw the bezier curve that is specified by this list of points.

The de Casteljau algorithm can be used to generate a single point that exists on the bezier curve. It is a recursive algorithm takes two parameters: A list of control points and a floating point value \(t\) in the range [0, 1]. The de Casteljau algorithm returns the point that is \(t \%\) along the bezier curve. To draw the entire curve, you will compute a fixed amount of evenly spaced points on the curve (which are computed by varying the value of \(t\) provided to the algorithm). You will then connect consecutive points along the curve using straight lines. By default, your program does not need to draw the control structure.

The de Casteljau algorithm can be expressed recursively using the following equations:

\[ \begin{eqnarray} de\_casteljau([ p_1 ], t) &=& p1\\ de\_casteljau([ p_1, \ldots, p_n ], t) &=& de\_casteljau([ linear\_interpolate(p_1, p_2, t), linear\_interpolate(p_2, p_3, t), \ldots, linear\_interpolate(p_{n-1}, p_{n}, t) ], t) \end{eqnarray} \]

Where t is the is a floating point value in the range [0, 1] representing the parametric distance, linear_interpolate finds the point at the specified parametric distance between two points, and the square brackets specify a list of points.

Pseudo Code

For Monday, March. 27th, you are required to provide pseudocode for the ENTIRE assignment. You are required to have at least one class: BezierPoint.

You should also pseudocode the "mainwindow" driver program, and create a list of functions you need for this driver program to run. For any function you need to define, make sure you list the Pre and Post conditions!

"Hacker" Prompt

1. Movable Control Points: Add the ability to modify a Bézier curve after it has been drawn by dragging its control points. When the user is dragging a control point, the Bézier curve should be redrawn every time the mouse drag call-back function is called.

2. de Casteljau Slider: One of the interesting things about the de Casteljau algorithm is the "recursive descent" that occurs in order to find a particular point on the true curve. While you likely were able to create the Bézier without having a good visualization of how it works. The actual process that is going on, however, is pretty cool looking.

   Add a QtSlider widget, that allows the user to chose a value from 0 to 1. This will represent the parametric distance t. This control structure should display how the t^th point of the curve was generated.