CPSC 170 A

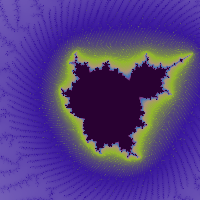
Mandelbrot

The Mandelbrot set is a set of complex numbers that remains bounded (does not increase to infinity) when iterated with a quadratic polynomial function. When the set is graphed on the complex plane, the set boundary has a complex pattern that does not simplify at any magnification and is therefore defined as a fractal.

Setup

Create a directory assignment7 under assignments in your cs170 directory. All code for the assignment should be stored in this directory.

  cd ~/cs170/assignments
  mkdir assignment7 
  cd assignment7

Details

The first part of this assignment is the creation of a class that represents complex numbers. Complex numbers are of the form (a+bi), where i is the mathematical imaginary number. For Mandelbrot, you will be required to have three operations: addition, multiplication, and magnitude (euclidean distance from the origin for the complex number). We have already written one of these classes earlier in the semester. You can either create one from scratch, or you may copy your old one into this project. MAKE SURE THIS IS FUNCTIONING BEFORE YOU CONTINUE!

Create a program that draws an image of the Mandelbrot set for complex numbers in the range \(-2 < a, b < 2\).To draw the set using Qt, you will need to convert window pixel x, y coordinates to complex a, b coordinates. For example, if the window is 200 by 200 pixels, the pixel (0, 0) would map to the complex coordinate (-2, -2) and the pixel (100, 100) to the complex coordinate (0, 0).

To draw the set, you need to define the color for every pixel. For each pixel in the window, set the color to a shade of gray depending on how many iterations of the quadratic polynomial function were required for the complex number's magnitude to exceed 2. The quadratic polynomial function can be defined recursively as:

\[ c_n = c_{n-1}^2 + c_0 \]

Where \(c_0\) is an initial complex number, that corresponds to a pixel in the image, and \(c_n\) is the n^th complex number computed with the quadratic polynomial function. What will \(c_{n - 1}\) be when computing \(c_1\)?

Note, since 255 is the largest number that can be represented with a gray-scale color, 255 is the maximum number of times that you need to iterate the quadratic polynomial function. For example, if the quadratic polynomial function is iterated 100 times before the absolute value becomes larger than 2, then set the pixel to be the color with the RGB values (100, 100, 100).

The real beauty of the Mandelbrot set is not the full image, but the inherent recursive structure that becomes apparent as you zoom in on pieces of the set. For this, you will want to write your functions that compute the set in such a way that the user can "specify" what locations to "zoom" in on within the image. To this end, your program should store 3 global variables: CENTER_X, CENTER_Y, and COMPLEX_WIDTH. If you set these variables to 0, 0, and 4 respectively, you will generate the whole mandelbrot set. Zooming in should just require changing these 3 values.

In order to implement this, the program should store the range of complex numbers that are currently being rendered in class attributes. The program should also have a method that converts pixel coordinates to complex coordinates using the current complex range instance variables. The following equations will convert between pixels coordinates and complex complex coordinates in a specified range:

\[ \begin{eqnarray} c_a &=& \frac{p_x}{W} \times (max\_a - min\_a) + min\_a\\ c_b &=& \frac{p_y}{H} \times (max\_b - min\_b) + min\_b \end{eqnarray} \]

Where c is the complex coordinate that corresponds to the pixel coordinate, p. W and H are the width and height of the window, and min and max are the current complex range of values.

Make sure you play around with different generations of the Mandelbrot set. Include a screenshot of your favorite image with your code submission. Make it a good one, because the best image in the class (as selected by an on-line poll) will be hung on my office door, and displayed on the course website. For the purposes of the competition, you should generate large images, on the order of 1000 x 1000 pixels. Allow plenty of time to generate your favorite images!

Pseudocode

For Monday, March. 20th, you are required to provide pseudocode for the ENTIRE assignment. You are required to have at least one class: ComplexNumber.

You should also pseudocode the "mainwindow" driver program, and create a list of functions you need for this driver program to run. For any function you need to define, make sure you list the Pre and Post conditions!

"Hacker" Prompt

Color Map: It is possible to create more visually pleasing images by using a color map to specify what color maps to which escape value. It is possible, for example, to have a color map between colors with RGB values \((100, 255, 150)\) and \((200, 50, 0)\) by interpolating between the two colors based on the escape value. It is possible to interpolate by using the linear interpolation equation we used in bezier, but use it with each of the color channels. For example, if the escape value is 128, then the interpolated color of the above two colors would be:
\[ \begin{eqnarray} r &=& (100 \times (1 - i)) + (200 \times i)\\ g &=& (255 \times (1 - i)) + (50 \times i)\\ b &=& (150 \times (1 - i)) + (0 \times i) \end{eqnarray} \]
where \(i = \frac{128}{255}\), which results in the following values:
\[ \begin{eqnarray} r &=& (100 \times (1 - 0.50196) + (200 \times 0.50196)) = 150.196\\ g &=& (255 \times (1 - 0.50196) + (50 \times 0.50196)) = 152.0982\\ b &=& (150 \times (1 - 0.50196) + (0 \times 0.50196)) = 74.706 \end{eqnarray} \]
It is also possible to produce a color map with more than two colors by first determining which pair of colors an escape value is between, and then interpolating the colors. For example, if a color map consists of three colors and the escape value is 42, then because \(\frac{42}{255}\) is less than 0.5 the interpolated color would be produced by interpolating between the first and second colors with \(i = \frac{42}{127}\).
Click, Click, Zoom: As you will no doubt be able to see, trying to find interesting locations in the Mandelbrot set with the above zoom capabilities is going to be difficult. You will have to manually convert from image pixels to complex numbers, and determine the zoom factor the same way.

However, there is an easier way. But it involves click handlers. Define a click handler that can get the location the user wishes to zoom in. You can also assume that each click will zoom in by a factor of 2. For the first click, the size of the complex plane becomes 2, ranging from (-1, 1) in both directions. You could also add a click handler for right clicks, which will zoom out, doubling the size of the square being generated.

This process will be faster than manually determining where to zoom, but is still is not going to be quick. Be prepared to wait several seconds (or minutes) between each click to see the new zoomed in location. The code for this, however, is pretty easy to implement.