< Back

Test 1

If you do not currently have a directory for tests, create one in your cs170 directory, and also create a directory for test1 

$ mkdir ~/cs170/tests
$ mkdir ~/cs170/tests/test1
$ cd ~/cs170/test/test1

This portion of the test is worth 50 total points. You may only access the Python documentation website and the tkinter documentation website. NO OTHER WEBSITES ARE PERMITTED. As usual, you are not allowed to directly copy any code from the Internet or another individual. You should also follow all coding standards discussed thus far.

Test 1

Question 8

In a file called question_8.py, create a program that creates a 400 × 400 window, and fills it with a target seen below. This target is centered in the window, and each circle is 75 pixels smaller than the enclosing circle.

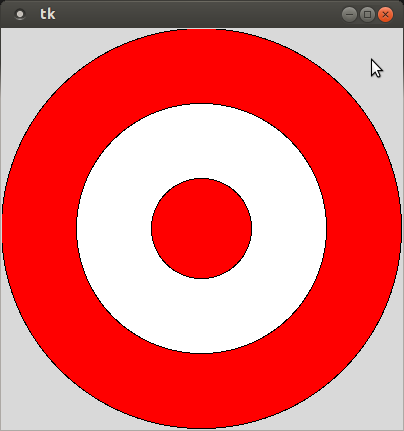
(10 points)

Question 9

In a file called question_9.py, create a program that will read in a text file representing a two-dimensional list. Your program should return True if all of the rows of the 2-dimensional list sum to the same value. 

test1.txt:
1 2 3
4 5 6
7 8 9

test2.txt
1 2 3
4 0 2
6 0 0

$ python3 question_9.py #using test1.txt
False
$ python3 question_9.py #using test2.txt
True
$

(10 points)

Question 10

In a file called questions_10_11.py, create a class called Simulator. This class should have attributes PC, R1, and R2. All three attributes should be integers, and should be defaulted to the value 0. This class should have methods called add and sub, which performs the specified operations on R1 and R2 (in that order, so R1 - R2), and stores the result in attribute R1. Each operation should increment the PC attribute by 1. You should also provide methods called set_R1 and set_R2, which allow the values of R1 and R2 to be set, respectively. 

  >>> my_sim = Simulator()
  >>> my_sim.set_R1(3)
  >>> my_sim.set_R2(4)
  >>> my_sim.add()
  >>> print(my_sim.R1)
  7
  >>> my_sim.sub()
  >>> print(my_sim.R1)
  3

(15 points)

Question 11

In the same file as above, create a class called AdvancedSimulator, which inherits your above definition of Simulator. This should add two additional attributes: R3 and R4. These should also be integers, but their values should be provdied to the constructor. You should define appropriate methods for setting these registers as well. You need to define methods to copy the value from R3 or R4 into R2. These methods should be named following the template copy_R#_to_R2. You also need to add two additional methods: mul and div, which computes the product and quotient (integer!) of R1 and R2 (respectively), and stores them in the R1 attribute. 

  >>> my_adv_sim = AdvSimulator(1, 2)
  >>> my_adv_sim.set_R3(2)
  >>> my_adv_sim.set_R1(3)
  >>> my_adv_sim.set_R2(4)
  >>> my_adv_sim.add()
  >>> print(my_adv_sim.R1)
  7
  >>> my_adv_sim.sub()
  >>> print(my_adv_sim.R1)
  3
  >>> my_adv_sim.copy_R4_to_R2()
  >>> print(my_adv_sim.R2)
  2
  >>> my_adv_sim.mul()
  >>> print(my_adv_sim.R1)
  6
  >>> my_adv_sim.div()
  >>> print(my_adv_sim.R1)
  3

(15 points)

 

 

Challenge

In a file called bonus_tk.py, write a simple program that fills an 800 × 800 tk window with a checkerboard pattern, as follows:

(5 points)

 

Challenge

Create a file called bonus.py to store this extra credit activity.

A polygon is simply a set of points that define the lines that complete an arbitrary shape. Tkinter gives us a mechanism through the create_polygon method of the canvas that allows us to create arbitrary polygons. All we have to do is provide a list of integers to the create_polygon method, and it will create that polygon on the screen.

For example, the following list of points can be used to create the following triangle on the tk window. 

  >>> points = [(400, 300), (500, 500), (300, 500)]
  >>> canvas.create_polygon(points)

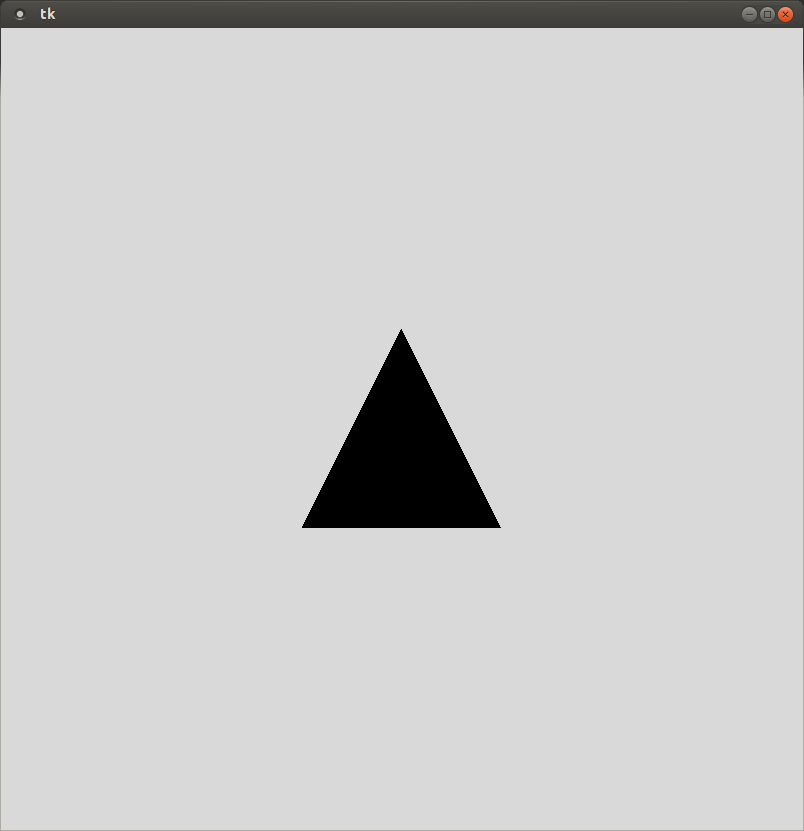
Create a class called Star, which at least has attributes x and y. It should also have a method called draw, which draws the star. You can assume some default size for your star. Given the x and y coordinates, you should compute the points necessary to draw a "traditional" 5-point star centered at the x and y coordinate specified on the canvas.

It is worth noting that create_polygon will connect the points in sequence, and will automatically connect the last dot with the first dot. You will need to specify the points in the order necessary to draw the shape shown below.

Treat the points of the star as if they exist on two separate circles, one for the inside points and one for the outside points. You just need to figure out how many degrees separate the points on the circle. Then you can use the trig identities to determine the x and y locations for the outside points and the inside points separately. Don't forget cos and sin need radians, not degrees.

(5 points)

Submission

When you have finished, create a tar file of your test1 directory. To create a tar file, execute the following commands:

cd ~/cs170/tests
tar czvf test1.tgz test1/

To submit your activity, go to inquire.roanoke.edu. You should see an available assignment called Test 1. Make sure you include a header listing the authors of the file.