

The z-buffer algorithm is used by graphics cards when rending 3D scenes to solve the visibility problem, determining which polygon to draw at a particular pixel.
Begin by creating a program that renders a 3D scene without solving the visibility problem, a wireframe rendering. A scene is simply a set of triangles defined in 3D, each vertex of a triangle has an x, y, and z coordinate. The file Triangles.tgz is a tar file that contains several text files that define scenes. Note that in these files each line represents the vertex of a triangle. The first three numbers of a line are the x y and z coordinates of a vertex. The last three are the red, green, and blue values for the color of the vertex. The first three vertices define a triangle and the next three after that another one, etc. Create a program that reads a triangle file, stores the data in a list (that you created in the last lab), and draws all of the triangles in a window. Each triangle should be drawn as an outline, not filled in. A few things to note:
Don't worry if the image this produces doesn't make sense, it is difficult to understand depth in a wireframe model without movement. To fix this you need to create the ability to rotate the scene. Add user interaction with the keyboard and or mouse to allow the user to rotate the scene. Be sure to include instructions to the user on how to control the rotation either through on an on screen display, or popup window. To rotate the triangles you will rotate each vertex about the x, y, or z axis by a specified amount. You can use the following equations:
xRotated = (x, y cos θ - z sin θ, y sin θ + z cos θ)
yRotated = (x cos θ + z sin θ, y, -x sin θ + z cos θ)
zRotated = (x cos θ - y sin θ, x sin θ + y cos θ, z)
Be careful when programming these equations that you do not change the x coordinate of a point and then use that new x coordinate to calculate the new y coordinate of the point. Lastly, give the user the ability to render the wireframe scene with solid triangles using the z-buffer algorithm when they have rotated it to a desired position. Again the program should inform the user how to perform this.
The z-buffer in the z-buffer algorithm is an array of z-values the same size as the dimensions of the window. Since the triangles are being projected onto the z=0 plane, the triangle that has the highest z-value at a particular pixel is the triangle that is visible. The color of a particular pixel is stored in a color-buffer that is the same size as the z-buffer. The algorithm iterates through all triangles in the scene computing the z-values for every pixel that intersects with the projection of the triangle. Any z-values that are larger than what is already stored in the buffer are recorded in the buffer along with the color of the particular triangle. After iterating through all of the triangles the colors that are stored in the color-buffer correspond to the visible pixels. The color-buffer can be written to the window by drawing each pixel using the fillRect method of the graphics class with a width and height of 1.
The z-values for each triangle can be computed using interpolation. The z-value for any point on the edge of a triangle can be computed by interpolating the z-value of the two points that make up the edge. The z-value for any point on a triangle can then be computed by interpolating the z-value of two edge points that it is in between.
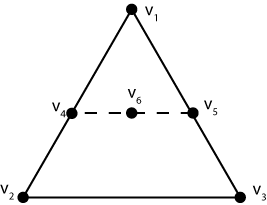
In the illustration above the coordinates of the point point v4 can be computed by interpolating the points v1 and v2 based on v4's y distance from v1 and v2. Likewise, the point v5 can be computed by interpolating the points v1 and v3. The point v6 can then be calculated by interpolating between v4 and v5 based on v6's x distance from v4 and v5.
Incrementing
The algorithm can be sped up by not having to interpolate three times for every pixel z-value that must be computed. Because the pixels are a fixed distance from each other the change in z-value from one pixel to the next on a particular line segment can be computed by dividing the change in z from one end-point to another by the number of pixels. Then, for each pixel on the segment, the interpolated point can be computed through by incrementing.
Gouraud Shading
The z-buffer algorithm can also be modified to simulate curved surfaces using Gouraud shading. Because each vertex of the triangle can have a different color, the color of a point in between two points can also be interpolated. The image of spheres at the top of this page illustrates the effect of interpolating colors.
Submission: Tar and submit your code on the course blackboard site.