CPSC 170 Lab 7: Recursion and Fractals

A fractal is a geometric figure that is self-similar in that any piece of the figure contains a miniature of the entire figure. Naturally, fractals fit nicely with the concept of recursion. There are lots of fractals that have interesting mathematical properties (and make pretty pictures); in this lab you will draw two of them, Sierpinski triangles and Koch snowflakes.

Sierpinski Triangles

A Sierpinski triangle (aka a Sierpinski Gasket) is a fractal that may be constructed as follows:

1. Draw a triangle.
2. Draw a new triangle by connecting the midpoints of the three sides of your original triangle. This should split your triangle into four smaller triangles, one in the center and three around the outside.
3. Repeat step 2 for each of the outside triangles (not the center one). Each of them will split into four yet smaller triangles. Repeat for each of their outside triangles.. and for each of the new ones.. and so on, forever. Draw a few rounds of this on paper to see how it works.

Your job is to write a Java program that draws a Sierpinski triangle. Think about the following:

• A Sierpinski triangle is a recursively defined structure -- each of the three outer triangles formed by joining the midpoints is itself a Sierpinski triangle.
• In practice you don't want to go on with the process "forever" as suggested above, so we'll limit how deep it goes. Define the depth of a Sierpinski triangle as the number of directly nested triangles at the deepest point. So a Sierpinski triangle consisting of a single triangle has depth 0; when a triangle is drawn inside of it, the resulting Sierpinski triangle has depth 1; when the three outside triangles have triangles drawn inside of them, the resulting triangle is depth 2, and so on. A depth of 10 or 11 gives a nice looking triangle in a reasonable amount of time. Smaller depths are interesting in that you can see more of the construction; higher depths generally take too long for casual viewing.
• A triangle is a polygon, so you can use the drawPolygon method of the Graphics class. Note: this method that it takes an array containing the x coordinates, an array containing the y coordinates, and an integer indicating how many points should be drawn (3 for a triangle).

The midpoint of a line segment can be calculated using interpolation. In order to find a point that is some fraction between the two points (x₁, y₁) and (x₂, y₂) the following equations can be used:

x_i = i * x₂ + (1 - i) * x₁
y_i = i * y₂ + (1 - i) * y₁

where i is a value between 0 and 1 that is the fraction of the distance between the two points that the point (x_i, y_i) is located. So, in order to find a point that is 1/2 between two points a value of i = 0.5 could be used.

The file SierpinskiTriangle.java contains the skeleton of a program to draw a Sierpinski triangle. The program has a slider that allows the user to specify the depth of the triangle that is drawn to the screen. The paint method simply calls the sierpinski method, which you must complete. The method should draw the triangle whose points were passed in, and then check to see if the desired depth has been achieved; if not, it should draw the triangle formed by the midpoints of the given points, then call itself recursively on each of the three new outer triangles. Try changing the color of the triangles and the location of the vertices. Use the slider to create fractal that you like. Use the Applications>Accessories>Take Screenshot application to create an image of the fractal and put it in your lab7 directory.

Koch Snowflakes

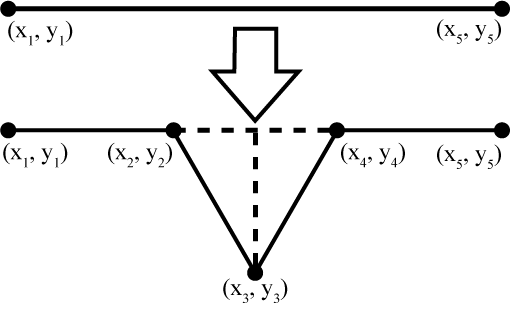
The Koch snowflake is a fractal generated by starting with 3 line segments forming a triangle (a Koch fractal of order 1). The algorithm for generating higher order Koch fractals involves splitting each line segment into three equal segments then replacing the middle segment by two line segments that protrude outward. The same algorithm is then recursively applied to each of the 4 new line segments. The diagram below illustrates the transformation of a segment.

In order to calculate the four line segments that represent the transformation of the segment defined by the points (x₁, y₁) and (x₅, y₅) the points that divide the segment into thirds, (x₂, y₂) and (x₄, y₄), must be calculated. These can be calculated using interpolation and the equations from the previous section of this lab.

The point that is the apex of the protrusion, (x₃, y₃), can be calculated with the following equations:

x₃ = x₁ + Δx / 2 - Δy * p
y₃ = y₁ + Δy / 2 + Δx * p

where

Δx = x₅ - x₁
Δy = y₅ - y₁

and p is a value between -1 and 1 that is the percent length of the original segment that the protrusion will be. That is, if p is 0.5 then the protrusion would be half the size of the segment from (x₁, y₁) to (x₅, y₅). If p is -0.5 then it would also be half the size of the segment, but protrude off of the other side of the segment. A value of one third of a segment length produces a nice looking fractal.

The file KochSnowflake.java contains the skeleton of a program to draw a Koch snowflake. The program has sliders that allow the user to specify the order and the size of the protrusion of the snowflake that is drawn to the screen. The paint method simply calls the koch method, which you must complete. The method should check to see if the desired depth has been achieved. If it has, it should draw the line of the given points. If it has not, then it should compute the four line segments that make up the next order and call itself recursively on each. Try changing the color of the triangles and the location and number of the initial lines. Use the sliders to create a fractal that you like. Use the Applications>Accessories>Take Screenshot application to create an image of the fractal and put it in your lab7 directory.

To submit your code: Tar the files in your lab7 directory and copy the tgz file to the directory /home/staff/bouchard/CPSC170A/lab7. Be sure to name the tar file with your names, not lab7.tgz.