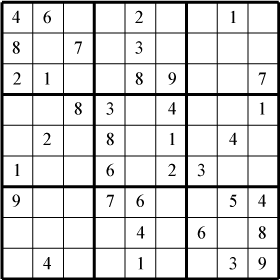

Sudoku is a puzzle that has been found in most newspapers since it gained popularity in 2005. Typically, the puzzle is played with a 9x9 grid that is subdivided into nine 3x3 boxes. The object of the puzzle is to fill the grid such that the digits 1 to 9 are contained (without repeats) in each row, each column, and each box. Seed digits are initially placed in the grid to define the puzzle and to limit where additional digits can be added by the person solving the puzzle. A puzzle is considered valid if the seed digits constrain the puzzle so that there is exactly one way to fill the remaining grid spaces. When trying to solve a Sudoku, people rely on logical reasoning to determine where certain digits can and cannot be placed in the grid. This is only fun when you are working on a valid puzzle. If there is more than one solution, it would be impossible to reason through; at some point you would have to guess. Clearly having no solution would be quite disturbing too. Is it possible to write a computer program that a) solves these puzzles and b) can discriminate valid puzzles from invalid ones? Yes - and you are going to write it!
Instead of trying to reason through the solution, you are going to use a brute-force approach to attempt to solve the puzzle. Begin by creating a class that represents a sudoku puzzle. Assume that puzzles are a 9x9 grid. Include an instance variable that represents a board, and a constructor that reads a file that represents a board. To display a sudoku puzzle, create a toString method. Test your class on the files in the tar file Puzzles.tgz. Note that empty cells have the value 0.
In order to solve a puzzle, you should create a method validMove that when given a row, a column, and a value to place into the specified cell, it returns true if the move is valid and false otherwise. This method would benefit from three helper methods that test each of the three conditions that would cause a move to be invalid.
Create a recursive method in the puzzle class that solves a puzzle by testing every possible move in every possible cell. The method should have parameters for the current cell and for the number to try in the current cell. It should also return true if it is able to solve the puzzle by setting the value specified by the parameters. If it is not possible to solve the puzzle by setting the value specified by the parameters the method should return the puzzle to the state it is in when it was called and return false. The recursion will be helpful, because if there is no move that produces a solution for a particular cell, then there is an error in a move that was previously performed. Recursion allows the program to backtrack to the problem easily. Finally, create a program that reads puzzle files and outputs a solution if there is one.
Submission: Tar and submit your code on the course blackboard site.
Looping
Replace the recursive solving method with a method that uses a stack and a loop. Compare the speed of the two methods using the System.currentTimeMillis method.
Validation
Create a recursive method that determines whether a puzzle is valid, that is it has only one solution. This function will be similar to the solving method. The program should be able to read a puzzle determine if it has a solution, and if it has one whether it is a unique solution.
Multiple Sizes
Modify the Puzzle class to read and solve puzzles of different sizes (2x2, 4x4, and 5x5 blocks are common).
GUI
Add a GUI front end that allows the user to solve the puzzle. The solver method can be used to determine if the user has made a move that will not lead to a solution or to give hints.