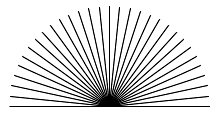
Lamp
Create a Python program that uses the turtle module to draw a fiber-optic lamp. Our digital representation of a fiber-optic lamp will simply be a set of lines of the same length, which converge upon a single point. There should be 31 lines evenly spaced out across the 180° necessary to draw the image.
Example
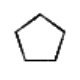
Polygon
A convex regular polygon is a shape that consists of a sequence of straight lines that all have the same length and meet at the same angle. Convex regular polygons can be parameterized according to the number of sides the shape has. For example, the convex regular polygons with 3, 4, and 5 sides are an equilateral triangle, a square, and a pentagon. As the number of sides increases, the polygons’ names get more complicated; for example, a 36-sided convex regular polygon is called a triacontakaihexagon.
Details
Create a Python program that uses turtle graphics to draw a convex regular polygon. It should prompt the user for the number of sides and the perimeter of the polygon it draws.
Example
Enter the number of sides:
5
Enter the perimeter:
100
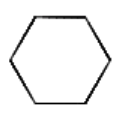
Enter the number of sides:
6
Enter the perimeter:
200
Hint
- Drawing a convex regular polygon is a lot like drawing a star; the turtle should repeatedly move forward and turn.
- Unlike the star, you will need to use a for loop to draw the polygon. Because the program must work for any number of sides, the number of times the turtle moves forward and turns may be different each time the program is run. Use the number of sides entered by the user, don't forget to make it an int, to control the number of times the loop runs.
- Just like drawing the star, the turtle will need to turn once for each corner of the polygon. So you can calculate how much it should turn because the sum of all of the turns will total 360°.
- Calculate the distance the turtle moves forward from the perimeter of the polygon. The turtle will travel the same distance every time, so the sum of every forward movement must be the polygon’s perimeter.
Challenge
As the number of sides in a convex regular polygon approaches infinity, it becomes a circle. Write a program that takes advantage of this to draw a circle. The program should prompt the user for the perimeter of the circle. Note that at some point, adding more edges to a polygon approximating a circle does not produce a better-looking circle, so the number of edges depends on the size of the circle. The program should calculate the number of edges needed to draw a perfect looking circle assuming that if all edges are 2 units long, the circle will look good.
Enter the perimeter:
200