CPSC120 - Activity 16

Absolute Value

Create a Python program that defines the function absolute(num: int) -> int that returns the absolute value of a number. The function should not use the math module’s fabs function.

Test Cases

import test

def absolute(num: int) -> int:
    # Put your code here.

def main() -> None:
    test.equal(absolute(1), 1)
    # Put more test cases here.
    return None

main()

Hint

Use a conditional statement to determine if num is negative.
The conditional statement’s body can’t return the absolute value because the function can only have one return statement, and it must be the last line of the function.
Instead, the function should return a variable that represents the absolute value of num.
Then the conditional body can set the variable’s value so that it will be returned when the function finishes.
The function should also handle if num is positive.

Minimum

Create a Python program that defines the function minimum(num1: float, num2: float) -> float that returns the minimum of two numbers. The function should not use the built-in min function.

Test Cases

import test

def minimum(num1: float, num2: float) -> float:
    # Put your code here.

def main() -> None:
    test.equal(minimum(1.0, 2.0), 1.0)
    # Put more test cases here.
    return None

main()

Hint

Use a conditional statement to determine if num1 is smaller than num2
The conditional statement’s body can’t return the smaller value because it can only have one return statement, and it must be the last line of the function.
Instead, the function should return a variable that represents the value of the smallest parameter.
Then the conditional body can set the variable’s value so that it will be returned when the function finishes.
There should also be an else statement or an if statement executed if num2 is smaller than num1.
What about if num1 equals num2? Does your program handle this case? Do you have a test case to verify that it does?

Point in Circle

Monte Carlo estimation uses random numbers to perform calculations. The technique is named after the casino because it depends on random chance and probability. We can use Monte Carlo estimation to compute the value of π by repeatedly testing whether a random point is inside of a circle.

Details

Create a Python program that uses the turtle to draw a large circle centered in the window. The program should generate random points in the window and draw them as a small x. The color of the x should be determined by whether or not the point is inside the large circle. If the point is inside the circle, the x should be green; if the point is outside the circle, the x should be red. Assume a point precisely on the edge of the large circle is inside the circle.

Example

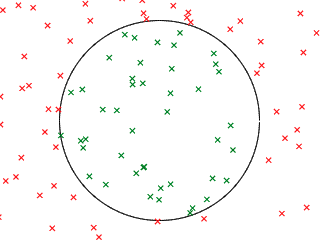
Point in Circle

Hint

Reusing functions makes programs more manageable to write! Paste the draw_x function to reuse it here. You can also adapt your code to draw a polygon to be a function and reuse that to draw the circle.
A point is inside a circle if the distance between the point and the circle’s center is less than the circle’s radius.
Finding the distance between two points is another opportunity to reuse functions. You probably wrote a function to compute the distance between two points in a previous assignment. Copy and paste that function into this program.

Challenge

To perform a Monte Carlo estimation of π, we need to estimate the area of the circle. Create a program that draws a large circle circumscribed by a square in the center of the window. That is, the square’s width and height are the same as the diameter of the circle. The program should generate a large number of random points. It should be possible for a random point to be located anywhere inside the square but nowhere outside the square. The fraction of points inside the circle estimates the circle’s area as a fraction of the square’s area. Since the area of a circle is π², the program can use the estimated area to solve for π.