< Back

Lab 6: Repetition

As usual, create a directory to hold today's files. All programs that you write today should be stored in this directory. 

$ cd ~/cs120/labs
$ mkdir lab6 
$ cd lab6

Practice Problem 1

Write a Python program which returns the factorial of a number specified in a variable called TO_COMPUTE. The factorial of a number \(n\) can be computed using the equation:

$$n! = n \times (n - 1) \times \ldots \times 1$$

Practice Problem 2

Write a program which computes computes the Nth power of 2, where N is a constant defined in the top of the file. You should not use the ** operator for this problem.

\[ 2^n = \underbrace{2 \times 2 \times \ldots \times 2}_{n} \]
Fibonacci

The Fibonacci sequence is a sequence of numbers that looks like:

$$1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, \ldots$$

Each number in the sequence, after the first two, is the sum of the previous two numbers in the sequence.

Details

In Emacs create a Python program in a file called fibonacci.py that prints the Fibonacci sequence. The program should prompt the user to enter the length of the series to print.

Your program does not need to worry about special cases where the user enters a number less than or equal to 0.

Example

$ python3 fibonacci.py
enter the sequence length: 8
1 
1 
2 
3 
5 
8 
13 
21

Hint

  • Because the program should work for any length sequence, you will need a loop to compute each of the numbers in the sequence.
  • What is different between this and other uses of an accumulator is that it needs the previous two iterations to compute the next iteration. To do this, keep two variables, one for the previous value and one for the one before the previous.
  • Pay attention to how the program will work for small numbers. If the user enters 1, the loop should run 1 times and print 1. If the user enters 2, the loop should run 2 times.

Challenge

One quirk about fibonacci numbers is their relation to right triangles. Starting with the number 5, every second fibonacci number represents the hypotenuse of a 3-4-5 right triangle. Three numbers of this form are referred to as a pythagorean triple. Create a new program called triples.py, which is a modification of the above program that asks the user for some number n, and prints the first n pythagorean triples.

Spirals

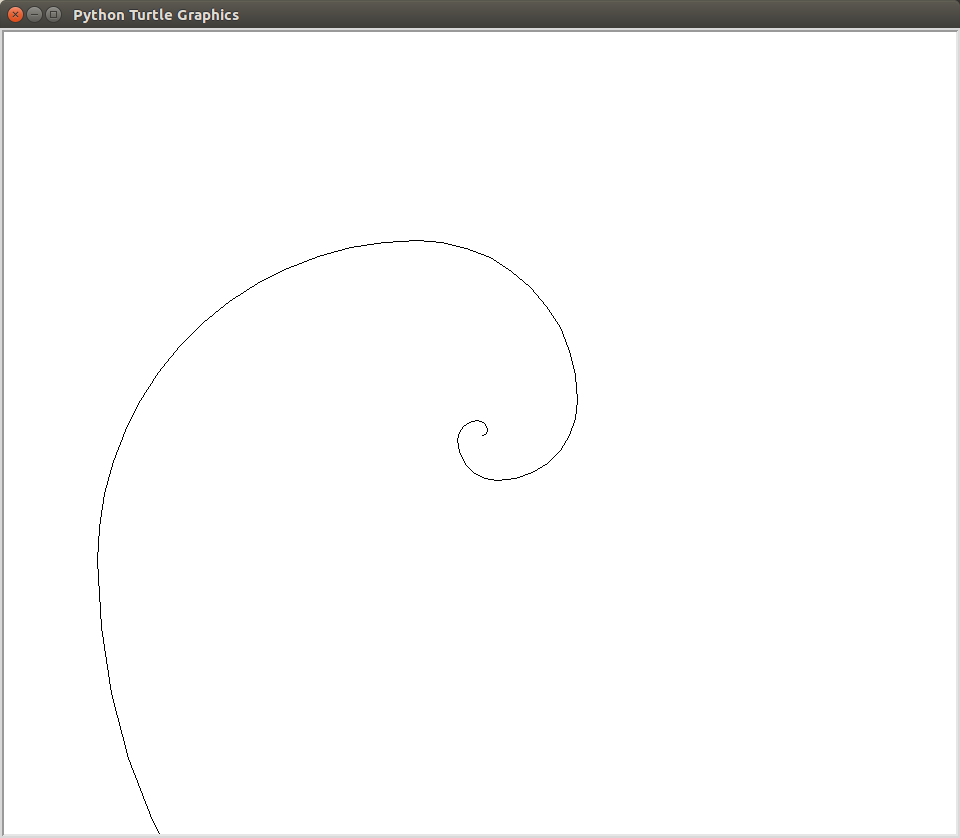
Last class, we saw how we could create a spiral by always moving forward by the same amount, and turning after each movement. This ended up with a spiral, which looked a little jagged (or really jagged). One way we can solve this problem is using circles in Turtle, and increasing the radius for each external circle.

Details

In Emacs create a Python program in a file called spiral.py that draws a circular spiral. The program should prompt the user the number of spirals to draw. You should draw a series of half-circles (created using pen.circle(radius, 180)). Each time a half circle is drawn, you should double the radius the next circle is drawn in.

Your program does not need to worry about special cases where the user enters a number less than or equal to 0.

Example

$ python3 spiral.py
Enter number of spirals: 8

Hint

  • Again, hard coding this shape will be impossible. You need to use a loop and the accumulator.
  • You won't be adding in this version of the accumulator. We want to be doubling the radius after each iteration, so we should be multiplying.

Challenge

Using the fibonacci sequence as the amount that the circle radii increase will result in a very cool looking spiral, as seen below. Modify your code to use the fibonacci sequence.

Fibonacci Spiral