< Back

Lab 14: Functions

As usual, create a directory to hold today's files. All programs that you write today should be stored in this directory. 

    $ cd ~/cs120/labs
    $ mkdir lab14 
    $ cd lab14

Practice Problem 1

Write the function minimum(number_1, number_2) that returns the minimum of the two parameters, number_1 and number_2. The function should not use the built-in min function. 




















  
Practice Problem 2



  Write the function clamp(number, minimum, maximum) that
  returns the result of clamping the specified number into the range
  $$[minimum, maximum]$$.  That is, if number is below
  minimum, it returns minimum,
  if number is above
  maximum, it returns maximum, and otherwise
  it returns number.  The function should not use the
  built-in functions min and max.




  

    
  

  

    
  

  









Point in Circle



  Earlier this semester we estimated pi using the Leibniz
  approximation. Another way of estimating the value of pi is to use
  Monte Carlo Estimation. The technique is named after the casino
  because it depends on random chance and probability. Before you can
  use the technique to estimate pi, you need a test for whether a
  given point is inside of a circle.



Details



  In a file called point_in_circle.py, write a program that
  allows the user to click in the window and draw small points.  The
  color of the points should be determined by whether or not the
  point is located inside of a larger circle.  If the point is inside
  the circle, the point should be drawn in green, if the point is
  outside the circle the point should be drawn in red.  Consider a
  point on the line to be inside the circle.




Example Output

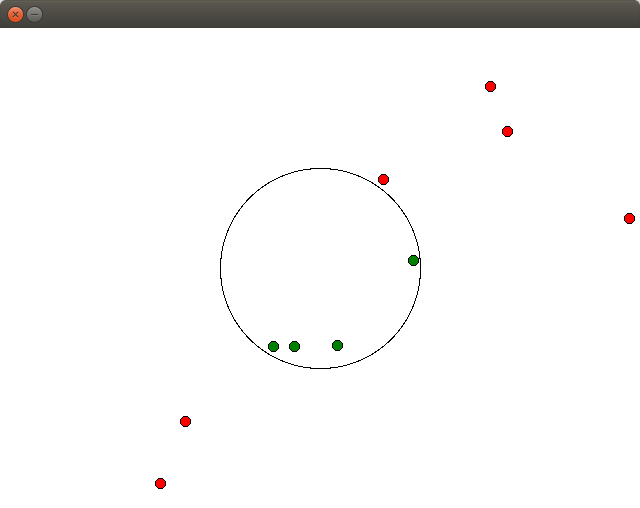
Turtle Drawing of a point in circle program



Hint



  
  

    
    
      
  • 
	
    
	  A point is inside of a circle if the distance between the point
	  and the center of the circle is less than the radius of the
	  circle.
	
    
	
    
	  The distance between two points can be computed using the
	  Euclidean Distance formula:
	
    
	
    $$d = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$$
    
	
    
	  Where \(d\) is the distance between the points \((x_1, y_1)\)
	  and \((x_2, y_2)\).
	
    
      
    • 
      
  • 
	You can
	use graphics.wait_for_button_press()
	to force your program to wait for the user to press a mouse button.
      
    • 
      
  • 
	
    You can use the x and y functions to get the coordinates of
	the mouse click.
	
    
      
    • 
    

  






  
Challenge

  

    To perform a monte carlo estimation of π, we need to estimate
    the area of the circle.  Create a square window in the graphics
    module, and draw a circle centered in this window as large as
    possible.  Generate a large number of random points, and keep
    track of which ones end up in the circle, versus the total number
    of points generated.  We can then estimate π using the
    following equation:
  

  \[
  \pi = \frac{4 \times points\_in\_circle}{num\_points\_generated}
  \]