< Back

Lab 8: Math Module and Fruitful Functions

As usual, create a directory to hold today's files. All programs that you write today should be stored in this directory. 

$ cd ~/cs120/labs
$ mkdir lab8
$ cd lab8

Sine Function

Hopefully you are familiar with the sine and cosine functions from back in your trigonometry class. As you can imagine, these are incredibly useful functions not only for mathematics, but for drawing in general. As it turns out, these function in the math module are Fruitful functions: they return the value they compute. Since these functions return their values, we can use those values in our drawings.

Details

Create the function draw_sin(amplitude) in a file called sine.py. The function should use the turtle module to draw a function plot of the math.sin function on the turtle window. The amplitude parameter is a scaling factor that tells you how much to inflate the value that the math.sin function returns.

You will have to modify the input and output of the math.sin function, so that the sine wave is visible on the turtle window. Make sure to test your function by calling the function multiple times with different parameters. Make sure your code follows the course's code conventions.

Example

You can place the follwing code at the bottom of your sine.py to check your work. 

draw_sin(25)
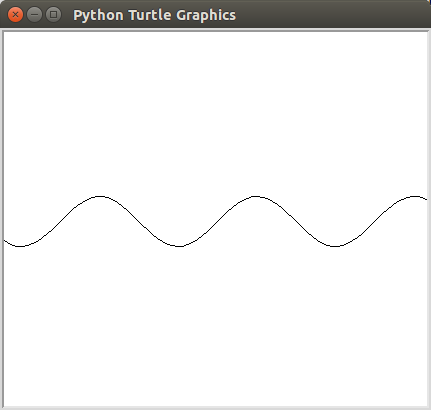
Turtle Graphics Sine Plot

Hint

  • You are going to approximate the sine wave curve by simply sampling the sine function. You are going to choose a set of equally spaced points on the curve. Use a for loop that starts at the left part of the window, and increases the value by a fixed step until it gets to the right portion of the window.
  • Treat the input to the math.sin function as the x coordinate of the point on the turtle window, and the return value as the y coordinate. You then simply have to goto each one of these points in a sequence.
  • The math.sin function always returns a value between -1 and 1. You need to use the amplitude parameter to increase the size of this output, so you can visually see the actual sine wave. You can do this by multiplying the output by amplitude.
  • To smooth the sine wave out, divide the input to the math.sin by the amplitude as well.

Challenge

The sine and cosine functions are interesting, but I think the tangent function is a much more visually appealing function. Change the color of the turtle's pen, and also plot the tangent function on top of the sine function.

Coin Counting

There are many people that would call me a lazy person. I don't find that offensive, but I think it's not a valid description. It's not that I'm lazy, I just try to be as efficient as possible. For example, in college a group of friends and I deduced the fewest amount of coins to carry that would produce any arbitrary amount of change. While a computation like that is still a little too complex, figuring out the fewest amount of coins for a fixed amount of change is possible.

Details

Create the function count_coins(cents) in a file called change.py. This function should take as a parameter the number of cents (an integer in the range 0 to 100) and returns the smallest number of coins (using the American monetary system consisting of quarters, dimes, nickles and pennies) necessary to make that amount of change.

Test your function by calling the function multiple times with different parameters. Make sure your code follows the courses code conventions.

Test Cases

Function Parameters Expected Output
0 0
1 1
2 2
5 1
10 1
15 2
16 3
25 1
50 2

Hint

  • While it might seem like you are going to use a loop for this function, you actually won't use a single loop.
  • You can use integer division (//) to determine how many times a coin goes into the change amount evenly.
  • Recall that you can use the mod (%) operator to determine the remainder of an integer division operator. Use this to determine the change amount the rest of the coins need to cover.
  • Start with the largest coin first (quarters) and work your way down. This is known as a greedy approach, and is very common in Computer Science.

Challenge

Going back to my inspiration for this activity, the perfect amount of change is going to be the maximum number that this function will produce on inputs in the range [0, 100). Once your function is written and tested well, compute the number of coins for all possible change values. Use the max function to find the largest number of coins.