Assignment 1: Simple DES
The Data Encryption Standard (DES) is a Feistel style cipher that became the US encryption standard in the 1980's. Today, DES is considered insecure, partially due to the relatively small key sizes required. The basics behind DES still apply to the new encryption standards, so knowledge of the workings of the algorithms is worth having.
Simple DES (S-DES) is an even more simplified version of the DES protocol. DES operates on blocks of size of 64 bits, while S-DES operates on blocks of 8 bits. Instead of a 56 bit key, the key for S-DES is only 10 bits long. And instead of 16 rounds, S-DES is only 2 rounds long.
The basic structure of SDES can be seen in Figure G.1 (Care of William Stallings supplementary materials). Figure G.1 shows three columns. The left column is the encryption functionality for S-DES. The right column displays the decryption mechanism for S-DES. The middle column is the key generation protocol for DES.
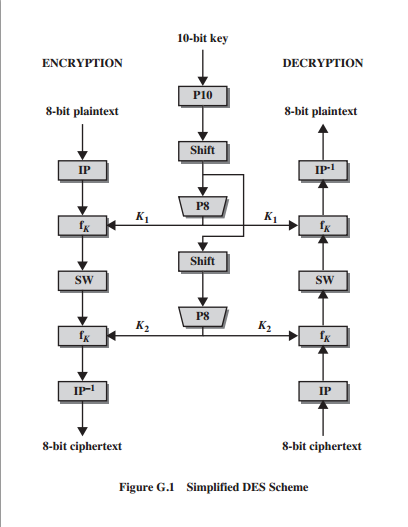
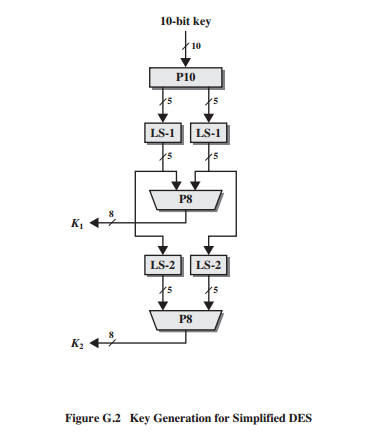
Figure G.2 (Again courtesy of William Stallings supplementary materials) shows off the key generation schemes for both rounds of the S-DES protocol. This is a deeper look at the center column of Figure G.1.
LS-# is a cyclic bitwise left shift. A simple bitwise left
shift can be accomplished using the << operator in
all languages referenced in this class. # refers to the number of
bits to shift to the left. LS-1 is a 1 bit shift, while LS-2 is a 2
bit shift.
P10 is a 10 bit permutation function. Let K = k0, k1, k2, k3, k4, k5, k6, k7, k8, k9 . P10(K) = k2, k4, k1, k6, k3, k9, k0, k8, k7, k5.
P8 is a 10 bit permutation function, that only returns 8 bits. Let K = k0, k1, k2, k3, k4, k5, k6, k7, k8, k9 . P8(K) = k5, k2, k6, k3, k7, k4, k9, k8.
IP is the Initial Permutation function. Similar to P10 and P8, it simply permutes the input bits. Let P = p0, p1, p2, p3, p4, p5, p6, p7. IP(P) = p1, p5, p2, p0, p3, p7, p4, p6.
IP-1 is the inverse of the Initial Permutation function. Let P = p0, p1, p2, p3, p4, p5, p6, p7. IP-1(P) = p3, p0, p2, p4, p6, p1, p7, p5.
fk is the most complicated part of the S-DES definition. The f function splits its input into two 4-bit halves, L and R. f can be defined as:
Where ⊕ is the bitwise exclusive or operation, and SK is the rounds subkey.
F is a mapping that takes a 4-bit input and an 8-bit round key. The construction of F contains 4 phases: Expansion and Permutation, key blinding, S-box randomization, and an additional permutation.
Let N = n0, n1, n2, n3. Then E/P(N) = n3, n0, n1, n2, n1, n2, n3, n0.
Key blinding involves XOR-ing the output of E/P with the round subkey. This is simply a bitwise XOR of the output of E/P.
The real black magic behind the security behind S-DES (and DES) is the use of the S-Boxes. These S-Boxes use 4-bits of the output of the key blinding phase to produce a 2-bit output, as defined by the S-boxes. There are two S-boxes, as seen below. Let P = p(0,0), p(0,1), p(0,2), p(0,3), p(1,0), p(1,1), p(1,2), p(1,3).
For S-box x, we will use values from P to choose a row and column in the specified S-box.
col = p(x,1) p(x,2)
S0
| 1 | 0 | 3 | 2 |
| 3 | 2 | 1 | 0 |
| 0 | 2 | 1 | 3 |
| 3 | 1 | 3 | 2 |
S1
| 0 | 1 | 2 | 3 |
| 2 | 0 | 1 | 3 |
| 3 | 0 | 1 | 0 |
| 2 | 1 | 0 | 3 |
As an example, let P = 11010010. For S0, row = 11 = 3 and col = 10 = 2. Therefore, the result of S0 is 3, or 11.
For S1, row = 00 = 0 and col = 01 = 1. Therefore, the result of S1 is 1, or 01
Finally, the output of the two S-boxes goes through one last permutation, P4. Let S = s0, s1, s2, s3. P4(S) = s1, s3, s2, s0.
The last piece left off is the switch function (SW). SW simply interchanges the left 4-bits and the right 4-bits. This assures that successive rounds operate on alternating instances of the input text.
This assignment is due Thursday, September 19th by the beginning of class. You may use any language that can execute on CS. However, if you chose a more esoteric language, I cannot help you. Submissions will be made through cseval.roanoke.edu.
Last modified: Thu Sep 12 09:23:06 EDT 2013